matematika
Minggu, 28 Januari 2018
Kamis, 25 Januari 2018
Teorema Terkait Sifat Aljabar Bilangan Real I
Sekarang kita akan membuktikan berbagai teorema yang berkaitan dengan sifat aljabar bilangan real. Sebagaimana kita ketahui bahwa analisis real membahas berbagai macam pola, sifat, teorema dan lain sebagainya yang dimiliki oleh bilangan real. Adapun analisisnya berupa pembuktian kebenaran dari teorema-teorema tersebut berdasarkan pembuktian matematika yang valid dan logis. Ingat bahwa pembuktian matematika menggunakan metode deduktif (dari khusus ke umum) yaitu dengan menggunakan pernyataan-pernyataan khusus yang sudah terbukti kebenarannya untuk menemukan pola umumnya. Dalam analisis real ini berarti bahwa kita membuktikan teorema yang ada menggunakan aksioma, teorema, atau pernyataan lain yang sudah terbukti kebenarannya sebelumnya.
Teorema yang kita bahas pertama terkait dengan penggunaan elemen 0 dan 1 sebagai berikut:Teorema 2.1.2
a. JikaDibacanya: jika z dan a anggota bilangan real dan z ditambah a sama dengan a, maka z sama dengan nol.
Dibacanya: jika u dan b anggota bilangan real, dan b tidak sama dengan nol, sehingga u dikali b sama dengan b, maka u sama dengan satu.
Dibacanya: Jika a adalah anggota bilangan real maka a dikali nol sama dengan nol.
Bukti
Dari pernyataan kita mempunyai  .
.
Akan dibuktikan bahwa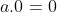
pembuktian:
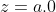 maka,
maka,
terbukti bahwa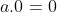
Akan dibuktikan bahwa
pembuktian:
terbukti bahwa
Langganan:
Komentar (Atom)