Bilangan Rasional dan Irasional

Salah satu bagian atau subset dari bilangan real adalah pasangan bilangan rasional dan irasional. Bilangan rasional adalah elemen bilangan real yang dapat ditulis dalam bentuk   dengan  dan . Bahasa sederhananya ialah bilangan yang dapat dibentuk menjadi bilangan pecahan. Dengan demikian maka bilangan rasional yang dilambangkan dengan 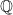 ini juga mencakup bilangan bulat (), bilangan asli (), dan bilangan prima (). Adapun bilangan yang tidak bisa ditulis dalam bentuk bilangan rasional inilah yang disebut bilangan irasional.

Berikut akan kita bahas beberapa teorema terkait kedua bilangan ini.

Teorema 2.1.4

Tidak ada elemen  sehingga 

Dibaca: tidak ada bilangan/elemen r anggota dari bilangan rasional, sedemikian hingga r kuadrat sama dengan 2

Teori ini menunjukan bahwa tidak ada bilangan rasional yang kuadrat hasilnya sama dengan 2 (coba cari). Hal ini juga berimplikasi bahwa tidak ada bilangan rasional untuk akar kuadrat dari dua. Dengan demikian menurut teori ini diperoleh bahwa bilangan  adalah bilangan irasional.

Sekarang kita akan membuktikan teori tersebut.

bukti

Untuk membuktikan teorema ini kita lakukan pembuktian secara tidak langsung menggunakan kontradiksi. Yaitu dengan mengandaikan negasi/kebalikan dari pernyataan sebagai berikut.

Pernyataan	Penjelasan
Andaikan ada elemen  sdemikian  hingga	Pengandaian negasi dari pernyataan
maka r dapat ditulis ,	definisi bilangan rasional ()
dengan p dan q tidak mempunyai faktor persekutuan selain 1	Pengandaian yang mengakibatkan keduanya terdiri dari bilangan genap dan ganjil
diperoleh  atau	diketahui dari pengandaian
adalah bilangan genap	karena  adalah bentuk bilangan genap
Karena  genap, maka p juga genap	Karena jika p ganjil, nilai  juga ganjil*. Jadi haruslah p genap
Karena p genap, maka dapat ditulis  untuk setiap	Definisi bilangan genap
Sehingga	Nilai kuadrat dari
Sebelumnya diketahui	Diketahui sebelumnya
Maka	Diketahui
	Diperoleh bahwa  bilangan genap
karena  genap, maka nilai q juga genap	Sama dengan p, Lihat bagian *

Berdasarkan pengandaian tersebut diperoleh bahwa p dan q adalah bilangan genap. Sedangkan menurut pengandaian dimana p dan q tidak mempunyai faktor persekutuan selain 1, artinya p dan q terdiri dari bilangan genap dan ganjil (tidak mungkin keduanya genap). Hal ini menimbulkan pertentangan (kontradiksi). 

Dengan kata lain pengandaian salah. Sehingga dapat disimpulkan bahwa yang benar adalah tidak terdapat bilangan  sdemikian hingga .

Keterangan:

Bilangan genap adalah bilangan yang dapat ditulis dalam bentuk 2a

Bilangan ganjil adalah bilangan yang dapat ditulis dalam bentuk 

*Andaikan p ganjil maka dapat ditulis  maka

Hal ini menunjukan bahwa  juga dapat dibentuk menjadi persamaan umum bilangan ganjil. Dengan kata lain jika p adalah bilangan ganjil, maka  juga bernilai ganjil.